| Issue |
Renew. Energy Environ. Sustain.
Volume 4, 2019
|
|
|---|---|---|
| Article Number | 8 | |
| Number of page(s) | 6 | |
| DOI | https://doi.org/10.1051/rees/2019005 | |
| Published online | 03 April 2019 | |
Research Article
Mathematical modeling of temperature effect on algal growth for biodiesel application
1
Department of Chemical Engineering, University of Bahrain, Zallaq, Kingdom of Bahrain
2
Academic Affairs and Scientific Research, Kingdom University, Riffa, Kingdom of Bahrain
3
Department of Chemical Engineering, King Fahd University of Petroleum and Minerals, Dhahran 31261, Saudi Arabia
* e-mail: zhossain@uob.edu.bh
Received:
7
November
2018
Accepted:
13
March
2019
Microalgae biomass is promising feedstock for the industrial production of biodiesel. Hence, research and development are required in various domains especially optimizations of growth conditions including temperature effect for mass scale operation (production of biomass, harvesting, extraction of lipid, etc). Since in middle east region, seasonal temperature variation and more rapid daily fluctuations are amenable to alter the growth kinetics of microalgae in outdoor culture and hence affect algae biomass production efficiency. Therefore, in this study, a mathematical model was developed to calculate how the algae sp. (Chlorella kessleri) will react at different temperatures. The model integrates Monod model and Arrhenius equation, and as such it describes the relationship of algal growth rate with culturing temperature and limiting nutrient concentration. The apparent activation energy and pre-exponential factors were calculated to be 2537 cal/mol and 0.0077 day−1, respectively. The developed models could be useful to anticipate the effective impacts of temperature on outdoor algae culture.
© S.M. Zakir Hossain et al., published by EDP Sciences, 2019
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The trend in recent years is replacing fossil fuels by liquid biofuels. First generation biofuels have achieved the required production rate economically. The energy source for this generation was food and oil crops including oil, sugar, maize and animal fats. It is obvious that the generation and consumption of liquid biofuels will remain the same and might grow in the near future. In general, the utilization of first-generation biofuels has formed several arguments, mainly because of their effect on international food markets and on food security, particularly with respects to the most vulnerable regions of the global economy. Relevant questions were appeared about their effectiveness and sustainability of their production. Second-generation biofuels produced fuels from the whole plant matter of dedicated energy crops or agricultural deposits, jungle gathering remains or lumber processing waste, rather than from food crops. However, the production technologies for the second-generation biofuel in the most part have not met the scales for commercial use and not attract with the market demand which has so far prevented any substantial exploitation [1]. For a technically and economically feasible fuel supply, some conditions must be satisfied: relatively cheap, should need low or no additional land usage, environmentally friendly and no contribution to air pollution, and should use minimal amount of water. Microalgae exploitation could achieve these requirements and therefore makes an important influence to meeting the main energy demand and, in the mean, while providing environmental assistances [2]. Microalgae are all unicellular and simple multi-cellular microbes, counting both prokaryotic microalgae, i.e. cyanobacteria (Chloroxybacteria), and eukaryotic microalgae, e.g. green algae (Chlorophyta), red algae (Rhodophyta) and diatoms (Bacillariophyta) [2–4]. Algae culture has several potential advantages that include: (i) uses non-arable land for their culturing so does not vulnerable to food security, (ii) provides high oil yield per acre (using microalgae yield of 10 000-gallon oil per acre compared with 625-gallon oil per acre for oil palm), (iii) has fast exponential growth and (iv) uses CO2, nitrogen, phosphorus and brackish/waste water during growth. As such, algae culture can contribute to CO2 biofixation, wastewater treatment and source of biofuel [5–12].
Generally, temperature, nutrient (nitrogen and phosphorus) concentration, light intensity, initial CO2 concentration and initial inoculum size are the parameters that affect the microalgae growth rate. Among these, temperature and nitrogen concentration are considered the main parameters. It is well known that models of cell culture are useful tools to predict growth kinetics as well as better information in aquatic resource management [13–15]. To our knowledge there is no mathematical model for Chlorella kessleri (one of the green microalgae sp.) available in literature. Therefore, this paper develops a mathematical model of C. kessleri growth at different temperature and nitrogen concentration. For this, both Monod model and Arrhenius equation were applied. The development of this model could open the opportunity to propose models of automated bioprocess control and optimize productivity at large scale, which in turn helpful for biodiesel production.
2 Materials and methods
2.1 Chemical and reagents
All the solvents and chemicals used were obtained from Sigma–Aldrich, unless stated otherwise.
2.2 Algae species and growth conditions
The microalgae species (C. kessleri) was obtained from Algae depot in the USA. The algae species was cultured in a media called Bold's Basal Medium (BBM), which was prepared based on the recipe shown in the Supplementary Table S1. The pH of the medium was adjusted to 7 by NaOH (0.1 M). The experimental setup for this study is shown in Figure 1. To avoid the lag phase, the microalgae species was initially pre-cultured and then moved into the photobioreactors (PYREX 1L Erlenmeyer flasks, working volume was 500 mL each). The initial concentrations of the microalgae strain were 2.2 × 107 cells mL−1. The photobioreactors were arranged on a bench, where Grolux fluorescents light bulbs (light intensity of 65 μmol m−2 s−1 measured by an LI-250 Light Meter) were placed above the water bath that regulates the culturing temperature. CO2–air mixture (96% air and 4% CO2) was fed at the bottom of the batch reactors.
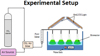 |
Fig. 1 Schematic diagram of the experimental setup used to cultivate microalgae. |
2.3 Measurement of algae biomass
For growth analysis, the algae samples (1 mL each) were obtained in every 24 h intervals. The cell concentration was calculated by measuring the absorbance at 690 nm using a UV-spectrophotometer (UNICAM). The dry biomass values (g/L) were obtained after vacuum filtration of 10 mL sample at every 3 days, with drying at 55 °C for 24 h. The biomass concentration (g/L) was estimated based on a biomass-optical densities standard curve (Supplementary Fig. S1).
2.4 Measurement of algae growth kinetic parameters
The specific growth rate (μ, or SGR, day−1) and biomass productivity (P, g
dw L−1 day−1) were determined from cell concentration and dry biomass weight data by using the following equations (1) and (2), respectively [15–20]: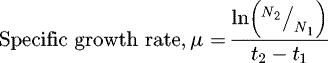 (1)
(1)
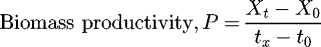 (2)where N
1 and N
2 are the biomass concentrations (g/L) at the beginning t
1 and at the end t
2 of the exponential growth phase, respectively; Xt
is the biomass concentration (g/L) at the end of the cultivation period tx
and X
0 the initial biomass concentration (g/L) at t
0 (day).
(2)where N
1 and N
2 are the biomass concentrations (g/L) at the beginning t
1 and at the end t
2 of the exponential growth phase, respectively; Xt
is the biomass concentration (g/L) at the end of the cultivation period tx
and X
0 the initial biomass concentration (g/L) at t
0 (day).
2.5 Determination of nitrogen removal efficiency
The removal of nitrogen efficiency was estimated by quantifying the level of removal (obtained by subtracting from initial to final values) from the culturing medium. The filtrate (obtained while performing biomass dry weight) was subjected to nitrate test using Chromo tropic acid method with acid persulfate digestion respectively according to procedure given in Hach Company, 2015 [21].
2.6 Development of mathematical models and validation
Mathematical model was developed to determine the quantitative linkage between environmental parameters (temperature, nitrate concentration in the medium) and cell growth kinetics. For simplification, prior to formulate model, the following assumptions were made: (i) light intensity was kept constant, (ii) initial inoculum size was kept constant and (iii) death kinetics were ignored. First, the effect of limiting nutrient (nitrate) on the growth of microalgae was described by the Monod model as shown in equation (3) [22].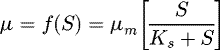 (3)where μ is the specific growth rate, day−1; μ
m
the maximum specific growth rate, day−1; S the limiting nutrient concentration, mg/L and K
s
the half saturation coefficient, mg/L.
(3)where μ is the specific growth rate, day−1; μ
m
the maximum specific growth rate, day−1; S the limiting nutrient concentration, mg/L and K
s
the half saturation coefficient, mg/L.
The maximum specific growth rate (μ
m
), which appears in the Monod model, is not a function of limiting nutrient concentration, rather, it is a function of temperature and light intensity. Since the light intensity was assumed constant, the maximum specific growth rate can be a function of temperature only and it may be described fairly by the Arrhenius equation (4) [22].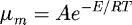 (4)where A is a constant, day−1; E the activation energy, cal/mol; R the universal gas constant, cal/K/mol and T the temperature, K.
(4)where A is a constant, day−1; E the activation energy, cal/mol; R the universal gas constant, cal/K/mol and T the temperature, K.
Upon combination of equations (3) and (4), equation
(5) was formulated, which can describe the growth of microalgae as a function of temperature and limiting nutrient concentration. (5)The half-saturation coefficient is an empirical value which can be found easily by plotting specific growth rate (μ) vs. nutrient concentration (S). It is important to note that Ks
is the substrate concentration at half maximal specific growth rate (μm
) and it depends on environmental conditions such as the temperature.
(5)The half-saturation coefficient is an empirical value which can be found easily by plotting specific growth rate (μ) vs. nutrient concentration (S). It is important to note that Ks
is the substrate concentration at half maximal specific growth rate (μm
) and it depends on environmental conditions such as the temperature.
For model validation, theoretical specific growth rates (computed using the model equation) vs. nutrient concentrations (S) were plotted for different temperature. These figures were compared with those obtained in experiment.
3 Results and discussion
3.1 Growth profile of microalgae sp. Chlorella kessleri
To characterize the time-resolved growth phase, it is important to explore the growth behavior of microalgae sp. C. kessleri in BBM at different culturing temperature. The population of C. kessleri grown at 25 °C in a batch photo-bioreactor containing BBM is shown in Figure 2. One can see from this figure that for 3 h incubation, the growth of C. kessleri was slow. The growth then continued to increase until day 9 before touching the stationary phase. The logarithmic growth phase was observed within 3–9 days and thereby maximum specific growth rates at different culturing temperature were determined in this region. Limiting nutrients concentration in the form of nitrate (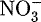 ) was monitored by plotting the nitrate concentration (mg/L) vs. time (day). The decreasing pattern of consumption of limiting nutrient, nitrate by C. kessleri, is shown in Figure 3. It is important to note that different growth and nitrate consumption patterns were observed at different culturing temperatures. As such, it is important to develop a model that describes the temperature effect on microalgal growth.
) was monitored by plotting the nitrate concentration (mg/L) vs. time (day). The decreasing pattern of consumption of limiting nutrient, nitrate by C. kessleri, is shown in Figure 3. It is important to note that different growth and nitrate consumption patterns were observed at different culturing temperatures. As such, it is important to develop a model that describes the temperature effect on microalgal growth.
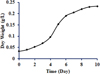 |
Fig. 2 Growth curve for microalgae sp. Chlorella kessleri in BBM at 25 °C in a batch bioreactor. |
 |
Fig. 3 Consumption of nitrate with time by Chlorella kessleri in BBM at 25 °C. |
3.2 Development of mathematical model for algal growth
In order to obtain the parameters of pre-exponential factor (A) and activation energy (E) in the Arrhenius model, maximum specific growth rate (μm
) was calculated for each temperature and the data were shown in Table 1. Figure 4 shows a plot of ln(μm
) vs. 1/T. It was a straight line with the R
2 value of 0.7621, indicating good fit. Since in biological system, the R
2 value should be more than 0.75 to validate the empirical model [23]. The A and E were calculated to be 0.0077 day−1 and 2537 cal/mol. Thus, Arrhenius model was rewritten with these values as: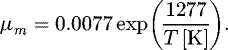 (6)
(6)
It is essential to note that negative activation energy was observed. The probable reason behind this is that increasing the temperature causes increase in the growth of algae to a certain level then decrease in the growth. The model (Eq. (6)) was used to anticipate the maximum specific growth rates. A comparison between experimental and predicted values of the maximum specific growth rates in terms of % errors is shown in Table 2. The maximum error between predicted and experimental specific growth rate was found less than 7%. Thus, the developed model was reliable.
The next step was to incorporate both temperature and nutrient concentration into one model. The nutrient limitation was modeled by finding the empirical coefficient of the Monod equation, which is the half-saturation coefficient (Ks
). The half saturation coefficient was found graphically from a plot of specific growth rate (μ) vs. nutrient concentration (S). Since the half saturation coefficient (Ks
) is a function of temperature, its values were determined for each temperature as shown in Table 3. A relationship between the half saturation coefficient and temperature is obtained by plotting Ks
(mg/L) vs. temperature (K) as depicted in Figure 5. Apparently, a second order polynomial relationship (as seen in Eq. (7)) was obtained for describing the effect of temperature on the half saturation coefficient. It is obvious from the figure that at moderate temperature the value of Ks
was relatively higher than that of both low and high temperature. Then, equation (7) was incorporated into the Monod model (Eq.
(3)), and a resultant model was obtained (Eq. (8)), that describes the specific growth rate as a function of limiting nutrient concentration.
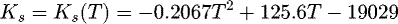 (7)
(7)
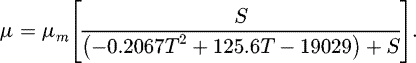 (8)
(8)
Finally, an integrated model was made (as shown in Eq.
(9)) by combining equations (8) and (6) and it describes the algal growth as a function of temperature and limiting nutrient concentration. This model was used to predict the specific growth rate for any temperature and nutrient concentration. The optimum temperature and nutrient concentration that will maximize the specific growth rate can also be measured.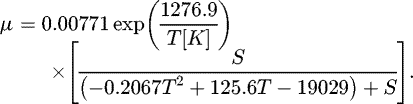 (9)
(9)
Data used to fit the Arrhenius model.
 |
Fig. 4 A plot of ln(μm ) vs. 1/T. |
A comparison between experimental and predicted maximum specific growth rates.
Half saturation coefficient at different temperatures.
 |
Fig. 5 The effect of temperature on the half saturation coefficient (Ks ). |
3.3 Model validation
The maximum specific growth rate was determined by model equation (6) that agrees satisfactorily with the experimental data for all temperature. For integrated model (Eq. (9)) validation, predicted specific growth rates vs. nutrient concentrations (S) were plotted for different temperatures, separately as shown in Figure 6A–C. These figures were compared with those obtained in experiment in the same figures. The predicted data are relatively deviated from the experimental values indicating fairly predictions in specific growth rate because these models are quadratic equations and are possibly inadequate to define the algal growth effectively in all kinetic regimes. Besides this model is solely a function of temperature and limiting nutrient concentration. Other important factors (e.g., light intensity, initial inoculum size, decay rate) that could possibly affect the specific growth rate of microalgae were ignored during model development.
 |
Fig. 6 A comparison between experimental and model prediction of specific growth rate (μ) at different temperatures: (A) 25 °C, (B) 35 °C and (C) 40 °C. |
4 Conclusions
In the present study, a mathematical model was formulated by combining Monod model and Arrhenius equation based on some assumptions. It describes the relationship of algal growth rate with culturing temperature and limiting nutrient concentration. This model was used to predict microalgal (C. Kessleri) specific growth rate at different temperatures. The apparent activation energy and pre-exponential factors were calculated to be 2537 cal/mol and 0.0077 day−1, respectively. The developed model agreed fairly with experimental data and could be useful to visualize the effective impacts of temperature on outdoor algae culture. However, to get a perfect prediction of growth rate by the model, it is important to develop a comprehensive model considering all possible factors such as culture temperature, nutrient (nitrate and phosphate), light intensity, initial inoculum size, CO2 uptake rate and death kinetics. Our research is underway in this direction.
Supplementary material
Supplementary Table and Figure. Access here
Acknowledgments
The authors would like to gratefully acknowledge the support provided by King Abdulaziz City for Science and Technology (KACST) through the Science & Technology Unit at King Fahd University of Petroleum & Minerals (KFUPM) for funding this work through project No. NSTIP # 13-WAT096-04 as part of the National Science, Technology and Innovation Plan.
References
- B. Liam, P. Owende, Renew. Sustain. Energy Rev. 14 , 557 (2010) [CrossRef] [Google Scholar]
- B. Wang, Y. Li, N. Wu, C.Q. Lan, Appl. Microbiol. Biotecnol. 79 , 707 (2008) [CrossRef] [PubMed] [Google Scholar]
- J. Cheng, Y. Huang, J. Feng, J. Sun, J. Zhou, K. Cen, Bioresour. Technol. 144 , 321 (2013) [CrossRef] [Google Scholar]
- M.G. de Morais, J.A.V. Costa, Biotechnol. Lett. 29 , 1349 (2007) [CrossRef] [Google Scholar]
- S.M.Z. Hossain, S.A. Razzak, M.M. Hossain, Chem. Eng. Technol. 41 , 1313 (2018) [CrossRef] [Google Scholar]
- S.M.Z. Hossain, A. Alnoaimi, S.A. Razzak, H. Ezuber, N.A. Bastaki, M. Safdar, S. Alkaabi, M.M. Hossain, Can. J. Chem. Eng. 96 , 1903 (2018) [CrossRef] [Google Scholar]
- M.A. Kazeem, S.M.Z. Hossain, S.A. Razzak, M.M. Hossain, Chem. Prod. Process Model. 13 , 20170082 (2018) [Google Scholar]
- P.M. Schenk, S.R. Thomas-Hall, E. Stephens, U.C. Marx, J. H. Mussgnug, C. Posten, O.R.J. Kruse, B.D. Hankamer, Bioenergy Res. 1 , 20 (2008) [CrossRef] [Google Scholar]
- G.C. Dismukes, D. Carrieri, N. Bennette, G.M. Ananyev, M.C. Posewitz, Curr. Opin. Biotechnol. 19 , 235 (2008) [CrossRef] [Google Scholar]
- K.B. Cantrell, T. Ducey, K.S. Ro, P.G. Hunt, Bioresour. Technol. 99 , 7941 (2008) [Google Scholar]
- Y. Chisti, Biotechnol. Adv. 25 , 294 (2007) [Google Scholar]
- S.A. Razzak, M.M. Hossain, R.A. Lucky, A.S. Bassi, H. De Lasa, Renew. Sustain. Energy Rev. 27 , 622 (2013) [CrossRef] [Google Scholar]
- D. Zhang, P. Dechatiwongse, E.A. del Rio-Chanona, G.C. Maitland, K. Hellgardt, V.S. Vassiliadis, Algal Res. 9 , 263 (2015) [CrossRef] [Google Scholar]
- J.E. Bissinger, D.J.S. Montagnes, Limnol. Oceanogr. 53 , 487 (2008) [CrossRef] [Google Scholar]
- C. Ocampo-López, S. Colorado-Arias, M. Ramírez-Carmona, J. Appl. Res. Technol. 13 , 498 (2015) [CrossRef] [Google Scholar]
- S.F. Mohsenpour, B. Richards, N. Willoughby, Bioresour. Technol. 125 , 75 (2012) [CrossRef] [Google Scholar]
- P. Das, W. Lei, S.S. Aziz, J.P. Obbard, Bioresour. Technol. 102 , 3883 (2011) [Google Scholar]
- M.G. De-Morais, J.A.V. Costa, J. Biotechnol. 129 , 439 (2008) [CrossRef] [Google Scholar]
- D. Tang, W. Han, P. Li, X. Miao, J. Zhong, Bioresour. Technol. 102 , 3071 (2011) [CrossRef] [PubMed] [Google Scholar]
- Y.S. Yun, S.B. Lee, J.M. Park, C.I. Lee, J.W. Yang, J. Chem. Technol. Biotechnol. 69 , 451 (1997) [CrossRef] [Google Scholar]
- Chromotropic Acid Method, Test ‘N TubeTM Vials, Hach Company, ed. 10 (2015) [Google Scholar]
- J.C. Goldman, E.J. Carpenter, Limnol. Oceanogr. 19 , 756 (1974) [CrossRef] [Google Scholar]
- P.D. Haaland, Experimental Design in Biotechnology (CRC Press, Taylor & Francis Group, Boca Raton, 1989) [Google Scholar]
Cite this article as: S.M. Zakir Hossain, Nader Al-Bastaki, Abdulla Mohamed A. Alnoaimi, Husny Ezuber, Shaikh A. Razzak, Mohammad M. Hossain, Mathematical modeling of temperature effect on algal growth for biodiesel application, Renew. Energy Environ. Sustain. 4, 8 (2019)
All Tables
All Figures
 |
Fig. 1 Schematic diagram of the experimental setup used to cultivate microalgae. |
| In the text | |
 |
Fig. 2 Growth curve for microalgae sp. Chlorella kessleri in BBM at 25 °C in a batch bioreactor. |
| In the text | |
 |
Fig. 3 Consumption of nitrate with time by Chlorella kessleri in BBM at 25 °C. |
| In the text | |
 |
Fig. 4 A plot of ln(μm ) vs. 1/T. |
| In the text | |
 |
Fig. 5 The effect of temperature on the half saturation coefficient (Ks ). |
| In the text | |
 |
Fig. 6 A comparison between experimental and model prediction of specific growth rate (μ) at different temperatures: (A) 25 °C, (B) 35 °C and (C) 40 °C. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


