| Issue |
Renew. Energy Environ. Sustain.
Volume 2, 2017
Sustainable energy systems for the future
|
|
|---|---|---|
| Article Number | 31 | |
| Number of page(s) | 7 | |
| DOI | https://doi.org/10.1051/rees/2017022 | |
| Published online | 08 September 2017 | |
Research Article
The suitability of the IEC 61400-2 wind model for small wind turbines operating in the built environment★
1
School of Engineering, The University of Newcastle,
Callaghan,
NSW
2308, Australia
2
School of Engineering and Information Technology, Murdoch University,
Murdoch,
WA
6150, Australia
* e-mail: samuel.evans@uon.edu.au
Received:
28
February
2017
Received in final form:
7
July
2017
Accepted:
27
July
2017
This paper investigates the applicability of the assumed wind fields in International Electrotechnical Commission (IEC) standard 61400 Part 2, the design standard for small wind turbines, for a turbine operating in the built environment, and the effects these wind fields have on the predicted performance of a 5 kW Aerogenesis turbine using detailed aeroelastic models developed in Fatigue Aerodynamics Structures and Turbulence (FAST). Detailed wind measurements were acquired at two built environment sites: from the rooftop of a Bunnings Ltd. warehouse at Port Kennedy (PK) (Perth, Australia) and from the small wind turbine site at the University of Newcastle at Callaghan (Newcastle, Australia). For both sites, IEC 61400-2 underestimates the turbulence intensity for the majority of the measured wind speeds. A detailed aeroelastic model was built in FAST using the assumed wind field from IEC 61400-2 and the measured wind fields from PK and Callaghan as an input to predict key turbine performance parameters. The results of this analysis show a modest increase in the predicted mean power for the higher turbulence regimes of PK and Callaghan as well as higher variation in output power. Predicted mean rotor thrust and blade flapwise loading showed a minor increase due to higher turbulence, with mean predicted torque almost identical but with increased variations due to higher turbulence. Damage equivalent loading for the blade flapwise moment was predicted to be 58% and 11% higher for a turbine operating at Callaghan and PK respectively, when compared with IEC 61400-2 wind field. Time series plots for blade flapwise moments and power spectral density plots in the frequency domain show consistently higher blade flapwise bending moments for the Callaghan site with both the sites showing a once-per-revolution response.
© S.P. Evans et al., published by EDP Sciences, 2017
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Small wind turbines (SWT) are designed for performance and durability based on International Electrotechnical Commission (IEC) standard 61400 Part 2 – Design requirements for small wind turbines [1]. The standard describes a wind field model, based on open terrain wind conditions to determine wind fluctuations and extreme wind events that can be used as input into aeroelastic codes to allow engineers to predict the performance and structural loading on the turbine for a given site wind condition.
Urban wind regimes are characterized as having low wind speeds with increased turbulent flow due to high surface roughness, atmospheric instability, interaction of the oncoming wind profile with surrounding obstructions, sudden changes in wind speed and direction, etc. [2,3]. Such environments induce stochastic variation in wind speed and turbulence intensity that is difficult to estimate. The existing wind field model in IEC 61400-2 appears to be inadequate when applied to turbines sited in the built environment since it does not incorporate all the design models and wind dynamics related to such highly turbulent sites. Not accounting for these salient features of urban environment can lead to overly optimistic predicted turbine power output [2] underestimated loads, high fatigue loading, and possible premature failure of turbine components [4,5]. For rooftop based small horizontal axis wind turbines, the rapidly fluctuating gust imposes high dynamic loading on the turbine and can cause resonance. Recorded turbine failures and poor, inconsistent performance in the built environment [6] suggests the inadequacy of IEC 61400-2 and calls for better understanding of the effects of elevated turbulence and loading issues on the performance of SWT.
IEC 61400-2 allows for the use of either von Karman or Kaimal spectral density functions to simulate the flow fields, calculate design loads and predict loadings on the turbine. Both of these turbulence models are based on the wind conditions pertaining to open terrain. Moreover, IEC 61400-2 designates small wind turbine operation into four classes that cover most operating sites. There is also a provision of an “S” class to address the special wind conditions, nonetheless the standard does not provide sufficient parameters to address the elevated turbulence levels in the built environment and thus cannot ensure acceptable reliability and safety levels for SWTs. IEC 61400-2 Annex [M], however, defines such “extreme urban wind conditions” as “other wind conditions” and advises that the standard wind condition model is no longer valid for use by the engineer without modification, yet it is purely an informative Annex and does not provide any alternative suggestions to model the urban wind conditions.
There has been some progress made from independent and collaborative studies related to characterization of turbulence and power curves of SWTs in the built environment [7–9], structural behaviour of wind turbines and design optimization [10,11], numerical analyses on turbine placement and effect of buildings/obstacles on oncoming wind profile [12–14,15]. Researchers at Murdoch University have studied the characteristics of the urban wind on a 1.5 kW swift wind turbine installed on the rooftop of a Bunnings Ltd. warehouse in the suburb of Port Kennedy (PK) in Perth Western Australia [3]. Part of their work was to investigate if the von Karman and Kaimal models are appropriate for use in the design of SWTs installed in the built environment, and to compare the assumed turbulent spectra with those of the actual flow conditions. The authors observed that both the standard models underestimated he magnitude of the measured values for all wind components and proposed a corrected Kaimal model for rooftop sites in the built environment. Researchers at the University of Newcastle (UoN) have created detailed computational models of SWTs operating in highly turbulent environments and have verified the accuracy of these models against experimental data obtained from an instrumented 5 kW Aerogenesis turbine [16]. Both groups have collected a significant amount of wind data at their respective sites.
The aims of this study are to compare the measured turbulent inflow wind conditions at two sites in the built environment with the modelled wind conditions from IEC 61400-2. The impact of these wind conditions on key turbine performance parameters is compared using a model of a 5 kW Aerogenesis turbine developed in the aeroelastic code Fatigue Aerodynamics Structures and Turbulence (FAST). This process is considered analogous to using aeroelastic codes to determine small wind turbine design loads from measured wind field conditions, compared to conditions simulated by the IEC standard.
2 Methodology
Wind data at two locations − Callaghan (UoN) in Newcastle, and PK in Western Australia − were gathered for a period of 6 months. Wind monitoring at PK was performed using an ultrasonic anemometer that gathered wind speed, wind direction, relative humidity and temperature at 10 Hz sample rate, with the wind data at Callaghan gathered using a cup anemometer and wind vane attached to a 5 kW Aerogenesis wind turbine tower, with data acquired at 1 Hz. Figure 1a and b shows an aerial view of the PK and UoN wind turbine sites with the red circle indicating a 500 m radius around the turbine, detailing the complex built environment terrain.
For the characterization of atmospheric wind fields and turbulence, the raw wind data from the anemometers were analysed in Matlab to compute the parameters of interest; the horizontal wind speed over the observation period was binned by wind speed, as a 10-min average, in conjunction with standard deviation with respect to the same time interval [17]. To characterize the turbulent velocity field and estimate dynamic loads, the probability density function of wind fluctuations is often expressed as a Gaussian distribution. The IEC 61400-2 standard uses a normal turbulence model (NTM) to describe turbulence and turbulence intensity, with the relationship between longitudinal turbulence and wind speed given by:
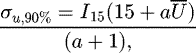 (1)
where I15 is the characteristic longitudinal turbulence intensity for
(1)
where I15 is the characteristic longitudinal turbulence intensity for 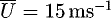 , a is a dimensionless slope parameter, and
, a is a dimensionless slope parameter, and  is the magnitude of the three-dimensional wind speed at the hub averaged over 10 min. The characteristic longitudinal turbulence intensity is expressed as the 90th percentile of longitudinal turbulence intensity measurements binned with respect to wind speed, assuming a Gaussian distribution. From IEC 61400-2, I15 and a are 0.18 and 2 respectively. These values are specified for all small wind turbine classes despite the fact they are site dependant. This simplification allows designers to use typical values instead of undertaking expensive monitoring campaigns at specific sites. Equation (1) thereby reduces to:
is the magnitude of the three-dimensional wind speed at the hub averaged over 10 min. The characteristic longitudinal turbulence intensity is expressed as the 90th percentile of longitudinal turbulence intensity measurements binned with respect to wind speed, assuming a Gaussian distribution. From IEC 61400-2, I15 and a are 0.18 and 2 respectively. These values are specified for all small wind turbine classes despite the fact they are site dependant. This simplification allows designers to use typical values instead of undertaking expensive monitoring campaigns at specific sites. Equation (1) thereby reduces to:
 (2)Equation (2) can be rearranged in terms of longitudinal turbulence intensity, Iu, as follows:
(2)Equation (2) can be rearranged in terms of longitudinal turbulence intensity, Iu, as follows:
 (3)
(3)
Equation (3) was proposed by Stork et al. [18] and is based on the assumptions of open terrain and hub-height wind speed ranging from 10 to 25 ms−1. Figure 2 shows the average 10-min wind speed and its longitudinal standard deviation at both PK and UoN. The mean and standard deviation of each 10-min averaged longitudinal velocity component were binned in wind speed bins of width 1 ms−1 centred on integer multiples of 1 ms−1. The 90th percentile fit of the measured data was calculated as:
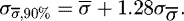 (4)
When compared with the IEC 61400-2 at 90th percentile of the standard deviation, IEC 61400-2 overestimates the measured data at lower wind speed (<4 ms−1) and underestimates at higher wind speed for PK, while underestimating the turbulence level for the majority of the wind speeds at UoN. Figure 2 also shows a number of extreme events with large standard deviation (
(4)
When compared with the IEC 61400-2 at 90th percentile of the standard deviation, IEC 61400-2 overestimates the measured data at lower wind speed (<4 ms−1) and underestimates at higher wind speed for PK, while underestimating the turbulence level for the majority of the wind speeds at UoN. Figure 2 also shows a number of extreme events with large standard deviation ( ) at both sites. The low turbulence at low wind speed evident in Figure 2a is likely due to inertial effects of the cup anemometer at low wind speeds. This occurs at wind speeds <2 ms−1, and is of little interest and consequence to a small wind turbine designer where the nominal rotor start-up speed of the Aerogenesis turbine is >4 ms−1.
) at both sites. The low turbulence at low wind speed evident in Figure 2a is likely due to inertial effects of the cup anemometer at low wind speeds. This occurs at wind speeds <2 ms−1, and is of little interest and consequence to a small wind turbine designer where the nominal rotor start-up speed of the Aerogenesis turbine is >4 ms−1.
Sampling at 10 Hz at the PK site rather than 1 Hz at the UoN site will more accurately capture the characteristics of the turbulence since it provides more data for higher order statistical analysis. Figure 2 is produced from 10-min averaged data, i.e. a 1 point (low order) statistical analysis, and so the differences in site sample rates are unlikely to be significant for the purposes of this comparison.
 |
Fig. 1 Location of the wind-monitoring site at the University of Newcastle (a), and Bunnings, Port Kennedy (b), with a 500 m radius indicated (Google Maps, 2016). |
 |
Fig. 2 90th percentile turbulence fit of measured data from: (a) University of Newcastle, (b) Port Kennedy, and IEC standard (fitted to both). |
2.1 Aeroelastic modelling
2.1.1 Development of the FAST model
In order to assess the effects of different inlet wind sets on turbine performance and loading, an aeroelastic model was developed for the 5 kW Aerogenesis wind turbine. This model was developed in FAST, which is a freely available and open source software package developed by National Renewable Energy Laboratory (NREL). Development of this small wind turbine model follows methodologies outlined in [19,20], with further details of this process found in [16,21].
Key to the development of this aeroelastic model is the input of aerofoil properties that govern rotor performance, turbine dynamics, and output power. The wind turbine blades consist of a constant SD7062 aerofoil section which has been designed for high-performance operation at low Reynolds numbers [22]. Typical operational Reynolds numbers range from 66,000 at the blade root during rotor start-up to 550,000 at the blade tip at rated wind speed conditions. Experimental lift and drag data for this aerofoil section only exist for the linear lift and drag region [23], whereas during turbine operation, much higher angles of attack can be achieved typically during yaw events or during rapid fluctuations in inlet wind speed. The lift and drag data were extrapolated for a full ±180° range of operation using the Viterna correction method within AirfoilPrep1 [24]. In a similar manner to the blade aerofoil data, the lift and drag data for the delta wing tailfin was input into the model using data presented in [25]; the tail fin is used as a means of passive yaw control to align the rotor plane to the direction of the inlet wind.
Structural parameters of the wind turbine blades and tower need to be inputted into the model. Both the blade and tower are considered to behave as cantilevered beams which are rigidly attached to the rotor hub and ground respectively. Inputs for these structural elements consist of sectional stiffness, linear density, and beam mode shapes which are used to deduce deflections and dynamic structural response. As the blades of this turbine are constructed from a glass-fibre composite consisting of various layers of uni-directional and bidirectional fibre, PreComp was used to calculate the effective stiffness by incorporating the net effect of different composite layups [26]. The wind turbine monopole tower consists of an 18 m octagonal section manufactured from AS4100 structural steel galvanized for environmental protection. Stiffness properties of the tower were also imported into FAST. Blade natural frequency mode shapes were determined using a Strand7 finite element software where a full model of the blade was subject to a rotational speed of 300 rpm and then solved for modal response. The changed natural frequency of vibrations and mode shapes were incorporated into the model.
Other parameters used for model input include the inertia of the rotor, drive train inertia, and inertia of the generator. Furthermore, the net mass and inertia of the nacelle about the tower axis were also a model input to determine yaw behaviour due to the tailfin aerodynamic response. This wind turbine utilises a self-excited induction generator (SEIG) which operates at variable rotational speed due to the implementation of a maximum power point tracking (MPPT) control algorithm. FAST does not natively allow for the use of this generator or control scheme, so a Simulink model was created and interfaced with FAST to facilitate the simulation of electrical power generation and the variable speed control effects on the rotor aerodynamics [27].
2.1.2 Initiation of simulations
A total of three 10-min simulations were undertaken to compare the response of the IEC Kaimal wind model to measured wind data from both the UoN and PK sites. A 10-min series was produced using TurbSim with a mean wind speed of 7.5 ms−1 and a turbulence level of 24% corresponding to the average annual wind speed of an IEC 61400-2 Class III wind turbine (which the Aerogenesis turbine was designed to be). Time series sets were selected from the 90th percentile longitudinal turbulence line-of-best-fit at a mean wind speed of 7.5 ms−1 for the UoN and PK wind data, meaning that all three wind sets effectively had the same 10-min mean wind speed, allowing for the effects of different site turbulence and wind spectra to be assessed. 7.5 ms−1 turbulence intensity was calculated at 34% and 29% for the UoN and PK sites respectively. While 10 min of operating data is significantly much shorter than the design life of the turbine − nominally 20 years − this time period is deemed acceptable as it allows for 10-min turbulence statistics to be compared, and is consistent with other studies that have studied structural loading using aeroelastic modelling [28].
Simulations were executed in FAST using the blade element momentum theory aerodynamic model, with inclusion of the Beddoes–Leishman dynamic stall model, Prandtl correction for tip-loss effects, and skewed wake correction to account for yaw errors. Simulation times had a significantly high simulation/real time ratio of up to 720, meaning that up to 5 days of central processing unit (CPU) time for a 10-min simulation. This lengthy computation time was due to a disparity in solver schemes between the fixed time step solver in FAST and the accelerated variable step solver used for the Simulink SEIG model, where the Simulink solver time step had to be reduced to the same time step as FAST.
3 Results
3.1 Ten-minute statistics
FAST allows for a wide range of outputs including, but not limited to; rotor aerodynamic power, tip speed ratio, generator electrical power, net rotor thrust and torque, blade and tower loads and deflections. The above parameters where output at a rate of 100 Hz and were read into a custom script for post-processing, and 10-min statistics such as mean, maximum and minimum, and standard deviation were output with respect to each inlet wind set.
Of key interest is generator electrical power output, and rotor tip speed ratio, as these parameters provide insight into the turbine’s performance. The Aerogenesis turbine has a nameplate electrical power output of 5000 W at a design wind speed of 10.5 ms−1, however Table 1 shows the 10-min mean power varies between 2077 and 2123 W for the wind inlet sets, due to the lower wind speeds in the built environments. Table 1 also shows a modest increase in mean power observed for the higher turbulent UoN and PK wind sets when compared to the IEC 61400-2 simulated data. When considering the ±standard deviation range, higher variation is observed in the UoN and PK wind sets. A similar trend is also observed when comparing tip speed ratio, where increases of the mean are likely due to the effects of rapid changes in wind speed in combination with rotor inertia and variable speed control effects. This indicates that variable speed control schemes for turbines used in complex terrain should be robust enough to contend with operation outside design tip speed ratios.
The effects of inlet wind sets on turbine loads were also considered, in particular: the net rotor thrust, net rotor torque, and the first blade flapwise moment (considered critical for fatigue loading). As documented in Table 2, the net rotor thrust load and blade flapwise load show a minor increase in mean load when comparing the IEC 61400-2 inlet wind to the UoN and PK wind series. Higher variations in ±standard deviation range were found for the thrust and flapwise load, indicating that higher turbulence can increase loading. Interestingly, mean rotor torque was practically identical, however higher variations in torque (and hence power) were experienced for the UoN and PK cases.
Table 3 shows a comparison of 10-min maximum loads for the three inlet wind sets with respect to net rotor thrust/torque, and blade flapwise moment. A significant increase in rotor thrust load of 69% and 24% respectively was observed for the UoN and PK wind inlet sets. A minor increase in rotor torque of 2% and <1% was found for the UoN and PK sets, indicating that the turbine controller performed well in optimising torque loading, possibly at the detriment of thrust loading. That is torque deviation beyond the design level was mitigated by the controller via reducing the rotor speed. This corresponds to a reduction in tip speed ratio, a decrease in aerofoil lift, and an increase in drag forces, which was ultimately manifest as an increase in net rotor thrust. In a similar manner to rotor thrust, an increase of 55% and 18% in flapwise bending moment was found for the UoN and PK wind sets. This represents a significant increase in loading which is likely to have consequences for both blade ultimate and fatigue loading.
Ten-min statistics for generator power and tip speed ratio.
Ten-min statistics for rotor thrust, torque, and blade load.
Ten-min maximum rotor loads.
3.2 Time series/PSD
A time series plot of the blade flapwise bending moment is presented in Figure 3, illustrating the output signals from FAST. Higher instantaneous loads are observed in both the UoN and PK inlet wind series when compared to the IEC 61400-2 wind series. A power spectral density plot, is provided to assess blade response in the frequency domain. Higher power spectral density (PSD) values at low frequencies were observed for the UoN and PK data sets, suggesting that the wind at UoN and PK has greater turbulent kinetic energy, with this energy passed on to the dynamics of the turbine. A once-per-cycle (1P) response was observed for all inlet wind conditions about the variable rotor operating speed of 3–4 Hz, with a lower magnitude 2P response observed (about 6–8 Hz). A higher magnitude 2P response was observed for the UoN set when compared to PK and IEC data sets, and a reduction in PSD magnitude was evident between 1 and 2 Hz. The exact cause of this reduction was not apparent and requires further investigation. No other significant dynamics effects, including natural frequency excitation, were observed.
 |
Fig. 3 Time series plot (a), and power spectral density plot (b), of blade flapwise response. |
3.3 Damage equivalent fatigue loads
Damage equivalent loads (DELs) were calculated for the blade flapwise bending moment load to compare potential for fatigue loading. Methodology was followed as per IEC 61400.13 [29] − measurement of mechanical loads − whereby the time series blade bending moment signals (Fig. 3a) were rainflow counted to deduce fatigue causing damage cycles, and converted to a single equivalent load that would induce the same damage as the entire fatigue spectra if applied for 20 years of operation at a frequency of 1 Hz. The IEC 61400-2 wind case produced a DEL of 181 Nm, whereas the PK and UoN wind inlet sets produced DELs of 286 and 201 Nm − an increase of 58% and 11% respectively.
4 Conclusions
The work documented in this paper clearly shows the assumed wind field spectral model used in IEC 61400-2 under predicts the level of turbulence for most wind speeds at the PK site and for all wind speeds at the UoN site. The measured data from both these built environment sites conclusively show that the turbulence is higher than 18%, the value assumed for small wind turbine sites in IEC 61400-2. The results of this study suggest that the IEC 61400-2 NTM is not applicable for built environment or complex terrain sites. Small wind turbine developers should therefore use caution when using IEC 61400-2 wind conditions for determining design loads.
A critically important point is the effect of these higher turbulence levels on turbine performance and fatigue loading experienced by a turbine throughout its nominal lifespan of 20 years. To address this, a detailed aeroelastic model of a 5 kW Aerogenesis turbine was developed in FAST using as input the measured wind sets from the PK and UoN sites as well as the assumed wind set from IEC 61400-2. The aeroelastic model also included, via a Simulink model, a model of the turbine’s self-excited generator and MPPT control algorithm, both of which are not native to FAST. Results of this modelling clearly show that for the same mean wind speed of 7.5 ms−1, higher turbulence at the UoN and PK sites increased the mean turbine power and operating tip speed ratio as well as increasing the ±standard deviation range. Mean rotor torque was largely unaffected by increased turbulence with both rotor thrust and flapwise moment increased by turbulence. Interestingly the predicted maximum rotor thrust for the UoN and PK sites were 69% and 24% higher than those from IEC 61400-2, with the predicted rotor torque within 2% of the IEC 61400-2 value. These results suggest the turbine’s control system optimised turbine torque at the expense of the rotor thrust load.
For SWT, the blade flapwise bending moment is the critical loading that determines the blade fatigue life. Predictions of damage equivalent fatigue loading for the turbine operating over 20 years, indicate the turbine at the UoN and PK sites experience 58% and 11% higher loading than for IEC 61400-2, suggesting shorter working life at both of these built environment sites when compared to IEC 61400-2.
Further research effort and site measurements are required to fully characterise the urban wind resource at a wider range of small wind turbine sites before a revision can be proposed to the standard. The influence of inlet wind conditions on small wind turbine operation is non-linear due to complex system dynamics. To fully investigate structural loading and fatigue life effects, aeroelastic simulations encompassing the full turbine operating range of wind speeds and turbulence levels will be required. This work will form the basis of future research effort.
References
- IEC 61400.2-2013, Wind Turbines Part 2. Design Requirements for Small Wind Turbines (Australia Standard: Australia, 2013) [Google Scholar]
- K. Sunderland, T. Woolmington, M. Conlon, J. Blackledge, Urban deployment of small wind turbines: power performance and turbulence, in Proc. 48th International Universities Power Engineering Conference, Dublin Institute of Technology, Ireland, 2–5 September 2013 (2013) [Google Scholar]
- A.B. Tabrizi, J. Whale, T. Lyons, T. Urmee, Extent to which international wind turbine design standard, IEC61400-2 is valid for a rooftop wind installation, J. Wind Eng. Ind. Aerodyn. 139, 50 (2015) [CrossRef] [Google Scholar]
- New Energy Focus, B. Windpower, UK field trial of building mounted wind turbines shows very poor results (2012), Available from: http://bergey.com/technical/warwick-trials-of-building-mounted-wind-turbines (last consulted on 2016/10/06) [Google Scholar]
- Nekon Pty. Ltd., Case Study: Wind Turbines Communications (2009), Available from: http://www.fontpr.com.au/how/case-study-wind-turbines-communications/ (last consulted on 2016/03/07) [Google Scholar]
- Warwick Wind Trails Final, Encraft (2009), Available from: http://www.warwickwindtrials.org.uk/resources/Warwick+Wind+Trials+Final+Report+.pdf [Google Scholar]
- A.-S. Yang, Y.-M. Su, C.-Y. Wen, Y.-H. Juan, W.-S. Wang, C.-H. Cheng, Estimation of wind power generation in dense urban area, Appl. Energy 171, 213 (2016) [CrossRef] [Google Scholar]
- J.L. Acosta, K. Combe, S.Z. Djokic, I. Hernando-Gil, Performance assessment of micro and small-scale wind turbines in urban areas, IEEE Syst. J. 6, 152 (2012) [CrossRef] [Google Scholar]
- L.C. Pagnini, M. Burlando, M.P. Repetto, Experimental power curve of small-size wind turbines in turbulent urban environment, Appl. Energy 154, 112 (2015) [CrossRef] [Google Scholar]
- A.B. Tabrizi, J. Whale, T. Lyons, T. Urmee, Designing small wind turbines for highly turbulent sites, in Solar2014: The 52nd Annual Conference of the Australian Solar Council, 8–9 May 2014, Melbourne, Australia (2014) [Google Scholar]
- J. Jeong, K. Park, S. Jun, K. Song, D. Lee, Design optimization of a wind turbine blade to reduce the fluctuating unsteady aerodynamic load in turbulent wind, J. Mech. Sci. Technol. 26, 827 (2012) [CrossRef] [Google Scholar]
- B. Wang, L.D. Cot, L. Adolphe, S. Geoffroy, J. Morchain, Estimation of wind energy over roof of two perpendicular buildings, Energy Build. 88, 57 (2015) [CrossRef] [EDP Sciences] [Google Scholar]
- K.K. Padmanabhan, Study on increasing wind power in buildings using TRIZ tool in urban areas, Energy Build. 61, 344 (2012) [CrossRef] [Google Scholar]
- H.N. Chaudhry, J.K. Calautit, B.R. Hughes, The influence of structural morphology on the efficiency of Building Integrated Wind Turbines (BIWT), AIMS Energy 2, 219 (2014) [CrossRef] [Google Scholar]
- I. Abohela, N. Hamza, S. Dudek, Effect of roof shape, wind direction, building height and urban configuration on the energy yield and positioning of roof mounted wind turbines, Renew. Energy 50, 1106 (2013) [CrossRef] [Google Scholar]
- S.P. Evans, D. Bradney, P. Clausen, Aeroelastic measurements and simulations of a small wind turbine operating in the built environment, J. Phys.: Conf. Ser. 753, 042013 (2016) [CrossRef] [Google Scholar]
- M. Hölling, A. Morales, J. Schneemann, T. Mücke, M. Wächter, J. Peinke, The relevance of turbulence for wind energy related research, in Progress in Turbulence and Wind Energy IV: Proceedings of the iTi Conference in Turbulence 2010 (2012), pp. 247–250 [Google Scholar]
- C.H.J. Stork, C.P. Butterfield, W. Holley, P.H. Madsen, P.H. Jensen, Wind conditions for wind turbine design proposals for revision of the IEC 1400-1 standard, J. Wind Eng. Ind. Aerodyn. 74–76, 443 (1998) [CrossRef] [Google Scholar]
- J.M. Jonkman, M.L. Buhl Jr, FAST User’s Guide (National Renewable Energy Laboratory, Golden, CO, 2005) [Google Scholar]
- D. Corbus, M. Meadors, Small Wind Research Turbine: Final Report (National Renewable Energy Laboratory, Golden, CO, 2005) [CrossRef] [Google Scholar]
- S.P. Evans. Aeroelastic Measurements, Simulations, and Fatigue Predictions for Small Wind Turbines Operating in Highly Turbulent Flow. PhD Thesis (School of Engineering, The University of Newcastle, Australia, 2017) [Google Scholar]
- P. Giguere, M.S. Selig, Low Reynolds number airfoils for small horizontal axis wind turbines, Wind Eng. 21, 367 (1997) [Google Scholar]
- C.A. Lyon, A.P. Broeren, P. Giguere, A. Gopalarathnam, M.S. Selig, Summary of Low-Speed Airfoil Data: Volume 3 (SolarTech Publications, Virginia Beach, Virginia, 1997) [Google Scholar]
- P.J. Moriarty, A.C. Hansen, AeroDyn Theory Manual (National Renewable Energy Laboratory, Golden, CO, 2005) [CrossRef] [Google Scholar]
- D.H. Wood, Small wind turbines: analysis, design, and application (Springer, 2011) [Google Scholar]
- G.S. Bir, User’s Guide to PreComp (Pre-Processor for Computing Composite Blade Properties) (National Renewable Energy Laboratory, Golden, CO, 2006) [CrossRef] [Google Scholar]
- D.R. Bradney, Measured and Predicted Performance of a Small Wind Turbine Operating in Unsteady Flow. PhD Thesis (School of Engineering, The University of Newcastle, Australia, 2017) [Google Scholar]
- S. Lee, M.J. Churchfield, P.J. Moriarty, J. Jonkman, J. Michalakes, A numerical study of atmospheric and wake turbulence impacts on wind turbine fatigue loadings, J. Solar Energy Eng. Am. Soc. Mech. Eng. 135, 031001 (2013) [CrossRef] [Google Scholar]
- IEC 61400.13-2015, Wind Turbines Part 13. Measurement of Mechanical Loads (Australia Standard: Australia, 2015) [Google Scholar]
https://nwtc.nrel.gov/AirFoilPrep (last consulted on 2017/01/07).
Cite this article as: Samuel P. Evans, Anup KC, David R. Bradney, Tania P. Urmee, Jonathan Whale, Philip D. Clausen, The suitability of the IEC 61400-2 wind model for small wind turbines operating in the built environment, Renew. Energy Environ. Sustain. 2, 31 (2017)
All Tables
All Figures
 |
Fig. 1 Location of the wind-monitoring site at the University of Newcastle (a), and Bunnings, Port Kennedy (b), with a 500 m radius indicated (Google Maps, 2016). |
| In the text | |
 |
Fig. 2 90th percentile turbulence fit of measured data from: (a) University of Newcastle, (b) Port Kennedy, and IEC standard (fitted to both). |
| In the text | |
 |
Fig. 3 Time series plot (a), and power spectral density plot (b), of blade flapwise response. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


