| Issue |
Renew. Energy Environ. Sustain.
Volume 1, 2016
|
|
|---|---|---|
| Article Number | 24 | |
| Number of page(s) | 4 | |
| DOI | https://doi.org/10.1051/rees/2016013 | |
| Published online | 15 June 2016 | |
Research Article
Dynamic thermal performance analysis of two solar air collectors with and without porous media
1 AL-FURAT AL-AWSAT Technical University, Najaf Technical College, Baghdad, Iraq
2 Faculty of Mechanical Engineering and Mechatronics, University POLITEHNICA of Bucharest, Bucharest, Romania
3 Faculty of Power Engineering, University POLITEHNICA of Bucharest, Bucharest, Romania
4 Faculty of Transports, University POLITEHNICA of Bucharest, Bucharest, Romania
⁎ e-mail: qahtan77@yahoo.com
The paper presents the thermal performance comparison between two types of solar air collectors, with and without porous absorber material. In order to simulate the transient processes which occur in the collectors two mathematical models were developed. Each model consists of a set of time dependent equations which describe the energy balance for the main components of the collector considering time-dependent thermo-physical properties and heat transfer coefficients. The theoretical models were validated by experimental data obtained from measurements performed in different meteorological conditions characteristic to the city of Bucharest – Romania (latitude 44°26′ N, longitude 26°6′ E). Good agreement between the simulation results and experimental data was achieved.
© Q.A. Abed et al., published by EDP Sciences, 2016
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Solar air heaters are one of the potential applications of solar energy in the world, such as space heating and drying of agricultural products. The suitable design is the key issue to a cost-effective solar air heater which leads to increased useful energy gain.
The basic types of the solar air collectors are the single pass with front duct or rear duct [1]. Several designs of solar air heaters have been proposed and discussed in literature. One of these designs is a double-pass flat plate solar air collector. The double-pass flow type of solar air collectors have been used to increase the heat-transfer area, which leads to improved thermal performance of the solar air collector [2,3]. Some studies [4] conducted a theoretically study based on the energy and exergy which clearly showed that increasing thermal energy between the absorber plate and the air through added the porous medium, improves the thermal performances of the solar collectors. The idea of using porous medium inside the lower channel leads to an increase in the thermal efficiency of the collector around more than 30% of the collector without porous medium. Thermal performance of solar air heaters with double-pass flat plate and “V”-corrugated absorber plate under recycle operation was investigated [5,6]. It was reported that the obtained thermal performance of “V”-corrugated collector is higher than that of the flat plate collector, due to turbulence air flow and higher heat transfer area provided by “V”-corrugated collector at the same air flow rates. The thermal performance of “V”-groove and cross-corrugated solar air collectors has been compared under a wide range of configuration and operating conditions [7]. The results show that the “V”-groove collector has lower performance compared to the cross-corrugated collector to which a transversely positioned wavelike plate was added to the bottom plate. The shape of the absorber plate in solar air collector is the most important parameter in the design of the collector. Moreover, the increasing of the absorber shape area will increase the heat transfer to the air [8,9].
The main objective of the present study is to investigate the thermal performance of two types of solar air collectors: “V”-corrugated porous absorber and “U”-single pass corrugated absorber, respectively. Transient mathematical models for these two types of solar air heaters operating under the same weather conditions are presented. In order to find the solution for the system of energy balance equations describing the two collector transient behaviour, a suitable computer program has been developed. To validate the theoretical model, comparisons between the experimental and theoretical results are made.
2 Description of the experimental set-up and measurement procedure
In this study, the experimental set-up was installed at Polytechnic University of Bucharest (44°26′ North, 26°6′ East). It included two geometrically similar collectors, one with “V”-porous absorber plate made of soft steel with two layers of a mesh wire (0.7 mm thickness) and the other with “U”-corrugated absorber plate made of aluminium (0.35 mm thickness) (Fig. 1). Both the collectors were placed together and facing southwards at an angle of inclination with the horizontal equal to 55°. The dimensions of the two collectors are 1.4 m × 0.7 m × 0.08 m. Single normal window glass of 3 mm thickness was used as cover for both collectors. The temperatures of the air inlet, outlet and inside the collectors were measured by 2, 4 and 16 thermal transducers distributed evenly, on the inlet, outlet and the bottom surface of the absorber plates, respectively at identical positions along the direction of flow for each collector. Two axial fans placed at the outlet of the collectors were used for air circulation. The air inlet section is positioned at the bottom of the collector and is moving upwards through the mesh wire of the porous collector type or through the single pass under the “U”-corrugated type.
 |
Fig. 1 The experimental set-up and the schematic assembly of the solar air heater with (a) mesh (porous) absorber and (b) “U”-corrugated absorber; (1) humidity transducer, (2) thermal transducers, (3) fin, (4) pressure transducer, (5) fan, (6) air inlet, (7) air outlet and (8) pyranometer. |
3 Mathematical modelling
A mathematical model for unsteady state conditions has been considered in the case of each collector. A system of three equations was derived to describe the energy balance on the air, absorber plate and glass (Fig. 2). It was considered that the air does not absorb solar radiation, the heat losses from the collectors back side are negligible, and the inlet air temperature is equal to the ambient temperature.
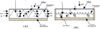 |
Fig. 2 Schematic diagram of through and single-glass solar air collectors: (a) with “V”-porous absorber plate and (b) “U”-corrugated absorber plate. |
3.1 Energy balance equations
The system of equations for each collector is composed of three ordinary differential equations representing the energy balance for the major components: Glass cover, absorber plate and air.
Hence, for the “V”-porous absorber collector in Figure 2(a), the system consists of equations (1) to (3), as follows:
The energy balance for the glass cover: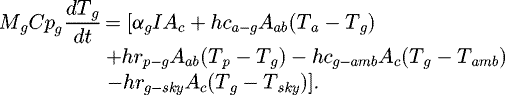 (1)
(1)
The energy balance for the air flowing inside the collector channel: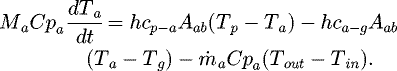 (2)
(2)
The energy balance for the absorber plate: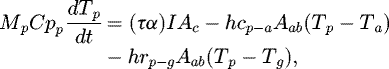 (3)where: t time [s], Tg, Ta, Tp, Tamb, Tsky, Tout and Tin temperatures of glass, air inside the collector, absorber plate, ambient air, sky, air outlet and air inlet respectively [K], αg glass absorptivity, I solar irradiance [W/m2], Ac and Aab collector aperture area and absorber plate area [m2], hca-g, hcp-a and hcg-amb convection heat transfer coefficient between the air and glass, plate and air, glass and ambient [W/m2 K], hrp-g and hrg-sky radiation heat transfer coefficient between the plate and glass, glass and sky respectively [W/m2 K], Mg, Ma and Mp mass of glass, air and absorber [kg], Cpg, Cpa, and Cpp specific heat of glass, air and absorber [J/kg K] and ma air mass flow rate [kg/s].
(3)where: t time [s], Tg, Ta, Tp, Tamb, Tsky, Tout and Tin temperatures of glass, air inside the collector, absorber plate, ambient air, sky, air outlet and air inlet respectively [K], αg glass absorptivity, I solar irradiance [W/m2], Ac and Aab collector aperture area and absorber plate area [m2], hca-g, hcp-a and hcg-amb convection heat transfer coefficient between the air and glass, plate and air, glass and ambient [W/m2 K], hrp-g and hrg-sky radiation heat transfer coefficient between the plate and glass, glass and sky respectively [W/m2 K], Mg, Ma and Mp mass of glass, air and absorber [kg], Cpg, Cpa, and Cpp specific heat of glass, air and absorber [J/kg K] and ma air mass flow rate [kg/s].
In a similar manner, we derived the equations for the “U”-corrugated absorber plate:
The energy balance for the glass cover: (4)
(4)
The energy balance for the air flowing inside the collector channel: (5)
(5)
The energy balance for the absorber plate: (6)
(6)
3.2 Heat transfer correlations
The convection and radiation heat transfer coefficients from the glass cover to the ambient and sky in equations (1) and (4) were calculated according to reference [10] (used for both types of collector). Also, the radiation heat transfer coefficient between the absorber plate and the glass in equations (1), (3), (4) and (6) have been calculated using expressions taken from reference [10] (used for both types of collector).
The Nusselt number used to calculate the convection heat transfer between the “V”-porous plate and air, hcp-a, has been determined with the following formula [11]: (7)
(7)
The Nusselt number for the convection coefficient, hcp-a, from the “U”-corrugated plate to air in the case of laminar flow (Rea < 2300) [12]: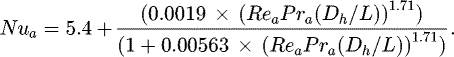 (8)
(8)
For transitional flow (2300 < Rea > 6000) [12]: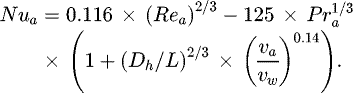 (9)
(9)
For turbulent flow (6000 < Rea, 10 < L/Dh < 400) [12]: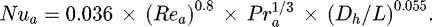 (10)
(10)
The thermal efficiency of the solar air collectors is defined as the ratio between the energy gain and the solar radiation incident on the collector: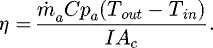 (11)
(11)
4 Results and discussions
The through pass “V”-corrugated porous absorber plate and single pass “U”-corrugated absorber plate solar air heaters are investigated both experimentally and theoretically under the same outdoor weather conditions of Bucharest characteristic to four days: 18.09.2014, 22.09.2014, 29.09.2014, 30.09.2014. The variation of measured average air temperature and calculated temperature of air, glass and absorber for the two types of collectors is presented in Figure 3. The air temperatures are very closely following each other thus, the mathematical model can accurately predict the behavior of the two collectors. In Figure 4 is presented the thermal efficiency both experimental and theoretical for the two collectors. The fitted values of thermal efficiency from the above equations are found to agree with the experimental data within ±2.03%. The heat losses from the solar collector were neglected which may add another source of error.
 |
Fig. 3 Comparison between the calculated and measured temperatures when ma = 0.33 kg/s, of (a) “V”-porous absorber plate and (b) “U”-corrugated absorber plate, on 22-09-2014. |
 |
Fig. 4 Comparison between the calculated and measured thermal efficiency: of (a) “V”-porous absorber plate and (b) “U”-corrugated absorber plate, on all four selected days. |
5 Conclusion
Two types of solar air collectors; with “V”-corrugated porous absorber and with “U”-corrugated absorber plate performance were investigated theoretically and experimentally. The air flow passing throughout the holes of the porous collector contribute to increase the surface per unit volume ratio and therefore increase the thermal efficiency in comparison with the “U”-corrugated collector. A mathematical model was derived and a case study has been performed for each collector type in Bucharest weather conditions. The theoretical results were validated by comparison with the experimental data; average errors equals to 7.75% and 10.55% for solar air collector with “V”-corrugated porous absorber and with “U”-corrugated absorber, respectively. The solar air heater with porous absorber performed better in all cases, having the advantage of expanded heat transfer area and enhanced turbulence air flow.
Acknowledgments
The author (Qahtan A. Abed) thanks the Ministry of Higher Education in Iraq.
References
- F.K. Forson, M.A.A. Nazha, H. Rajakaruna, Energy Convers. Manag. 44, 1209 (2003) [CrossRef] [Google Scholar]
- Y. Ho-Ming, H. Chii-Dong, L. Chi-Yen, Energy Convers. Manag. 41, 971 (2000) [CrossRef] [Google Scholar]
- H. Chii-Dong, Y. Ho-Ming, C. Tsung-Ching, Int. Commun. Heat Mass Transf. 38, 49 (2011) [CrossRef] [Google Scholar]
- E.M. Languri, H. Taherian, K. Hooman, J. Reise, Int. J. Green Energy 8, 643 (2011) [CrossRef] [Google Scholar]
- P. Dhiman, S. Singh, Int. J. Sustain. Energy 34, 1 (2015) [CrossRef] [Google Scholar]
- M.A. Karim, E. Perez, Z.M. Amin, Renew. Energy 67, 192 (2014) [CrossRef] [Google Scholar]
- L. Tao, L. Wenxian, G. Wenfeng, X. Chaofeng, Int. J. Green Energy 4, 427 (2007) [CrossRef] [Google Scholar]
- A.E. Kabeel, K. Mecarik, Renew. Energy 13, 121 (1998) [CrossRef] [Google Scholar]
- L. Wenxian, G. Wenfeng, L. Tao, Appl. Therm. Eng. 26, 1043 (2006) [CrossRef] [Google Scholar]
- W.H. McAdams, Heat transmission, 3rd ed. (McGraw-Hill Book Company, New York, 1954) [Google Scholar]
- H. Chii-Dong, L. Chun-Sheng, Y. Chuan Chuang, C. Chun-Chieh, Renew. Energy 57, 479 (2013) [CrossRef] [Google Scholar]
- B. Benamar, S. Rachid, in The 1st National Conference on Renewable Energies and their Applications 18 to 19 February 2014, Algeria (2014) [Google Scholar]
Cite this article as: Qahtan A. Abed, Adrian Ciocanea, Iuliana Soriga, Dorin L. Buretea, Viorel Badescu, Dynamic thermal performance analysis of two solar air collectors with and without porous media, Renew. Energy Environ. Sustain. 1, 24 (2016)
All Figures
 |
Fig. 1 The experimental set-up and the schematic assembly of the solar air heater with (a) mesh (porous) absorber and (b) “U”-corrugated absorber; (1) humidity transducer, (2) thermal transducers, (3) fin, (4) pressure transducer, (5) fan, (6) air inlet, (7) air outlet and (8) pyranometer. |
| In the text | |
 |
Fig. 2 Schematic diagram of through and single-glass solar air collectors: (a) with “V”-porous absorber plate and (b) “U”-corrugated absorber plate. |
| In the text | |
 |
Fig. 3 Comparison between the calculated and measured temperatures when ma = 0.33 kg/s, of (a) “V”-porous absorber plate and (b) “U”-corrugated absorber plate, on 22-09-2014. |
| In the text | |
 |
Fig. 4 Comparison between the calculated and measured thermal efficiency: of (a) “V”-porous absorber plate and (b) “U”-corrugated absorber plate, on all four selected days. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


