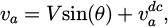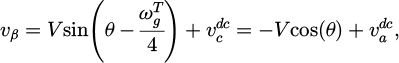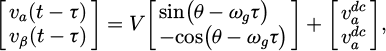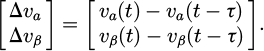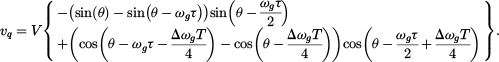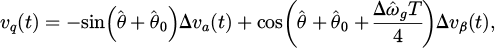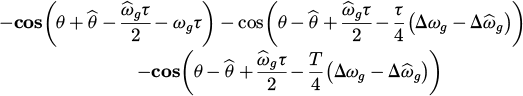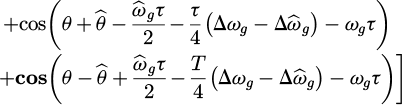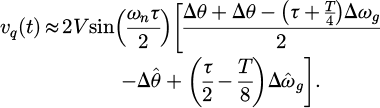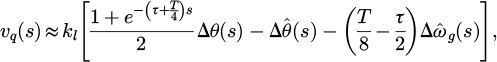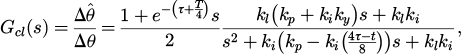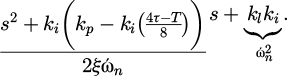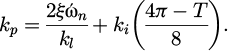© M.A. Bany Issa et al., Published by EDP Sciences, 2024

1 Introduction

Non-renewable energy sources have been heavily used to provide the world's energy needs for many years. However, their use is limited by various factors, including pricing, economic, political, and environmental issues [1,2]. According to the International Energy Agency (IEA), 72% of the world's energy is produced using fossil fuels in 2020 [3]. The adverse effects of depending on non-renewable resources have sparked growing concerns about their role in contributing to global warming, climate change, and environmental pollution. As a result, the scientific society is actively working towards reducing our dependence on these sources and transitioning to environmentally friendly renewable choices [1]. Notable examples of renewable sources include wind, geothermal, hydropower, and solar energy. Many countries rely on Renewable Energy Sources (RES) to produce electricity, for example, in 2021 Spain generates about 48.4% of its total energy from RES [4]. This means that the world is steadily shifting towards maximizing the utilization of renewable resources.

Synchronization techniques are employed to achieve fast and accurate grid synchronization between power electronics converters and the grid. Phase Locked Loop (PLL) algorithms are probably the most popular and widely used techniques for grid synchronization owing to their robustness and effectiveness [5–9]. Several research were done in designing PLLs for grid synchronization [5–20].

In general, the PLL consists of three main parts [6,8,10,16]; the Phase Detector (PD), the Loop Filter (LF), and the Voltage-Controlled Oscillator (VCO) (see Fig. 1).

The PD plays a central role in the PLL. It is reliable for generating a phase error signal, which represents the difference between the actual and the estimated phases. By comparing the phase of input reference signal with the feedback signal from the VCO, the PD calculates the phase error and provides an output signal that drives the control mechanism of the VCO.

The LF in the PLL is executed as a Proportional Integrator (PI) controller. It's a primary function to quell disturbances within the control loop of the PLL. Utilizing a combination of PI control actions, the LF smoothest the output from the PD, ensuring a stable and continuous control signal for the VCO. The filtered signal proceeds through the VCO to estimate the grid phase in different conditions accurately.

The VCO is the final part of the PLL, which generates an output signal with a frequency that can modified based on the control voltage received from the LF. As the control voltage changes in response to the phase error, the VCO frequency will be changed. This frequency adjustment allows the output signal to lock onto the frequency and phase of the input signal, ensuring synchronization in the PLL.

Recently, researchers have conducted several sorts of single-phase PLL research, and numerous single-phase PLL variants have been proposed and examined. The most popular techniques for creating an orthogonal signal include the Inverse Park Approach (IPA) [21], Transfer Delay (TD) [10,22,23], Second Order Generalized Integrator (SOGI) [15–17,24,25], Kalman Filter (KF) [14,26], All-Pass Filter [18,19], and Moving Average Filter (MAF) [27].

Synchronization issues were brought on by the presence of (DC-offset) in the PLL's input, which can be summed up as causes oscillations in the estimated fundamental grid phase, frequency, and amplitude. Additionally, the stability of the closed-loop system will be affected [6,9,11]. The use of Analog/Digital (A/D) conversions, digital controllers, the implementation of control algorithms in microcontrollers, sensors offsets, geomagnetic events, and grid failures can all contribute to DC-offset in grid synchronization [6,11].

Many types of research are done to reject the DC-offset in the input of PLLs. In [11], the DC-offset is removed by delaying the αβ-voltage signals, and the αβ signals are subtracted from the delayed version of the signals, it's a simple and effective way to remove the DC-offset in a three-phase Synchronous Reference Frame (SRF)-PLL system.

Numerous SOGI-based PLLs have been evaluated to determine their effectiveness in rejecting DC offset during grid synchronization [25]. These methods comprise the cascaded SOGI-PLL, modified SOGI-PLL, αβDSC with SOGI-PLL, in-loop dq-frame DSC, and complex-coefficient filter. Moreover, all these PLLs suffer from slow dynamic responses, and their closed-loop transfer functions are third order, which adds complexity to the process of designing appropriate controllers.

In [27], the MAF is employed as a prefilter in the αβ-reference frame, resulting in a faster response due to the lack of loop delays. However, when operating under off-nominal frequencies, this approach presents a phase shift, necessitating the creation of a phase error correction mechanism, which increases the system's complexity. Another option for the window length is to set it to half of the nominal period. This option can increase the speed of the response in general, it affects the filtering capability, making it challenging to reject DC offset effectively as the window length decreases.

The authors in [28] proposed an enhanced time-delay-based current decomposition method for single-phase Active Power Filter (APF) applications. They utilize a prefilter integrated Time Delay-based Orthogonal Signal Generator (TD-OSG) configuration for the dq-SRF and Reference Current Extraction (RCE). However, the authors use a fixed delay length in their nonadaptive time-delay method, which may limit the adaptability of the system to changes in the grid frequency.

In [6], the authors proposed a novel single-phase PLL approach named the non-adaptive DC immune DCI PLL. This technique involves utilizing the DSC operator to reject the effect of DC offset and the TD operator to generate orthogonal signals. Additionally, a feedback control mechanism was employed to address phase errors deriving from the delay used in DC offset rejection.

The authors in [8] proposed a novel PLL algorithm tailored for single-phase applications, specifically focusing on efficient DC offset rejection in grid voltage. The algorithm employs two delay operators to reject the DC offset effect and ensure orthogonality.

An Enhanced PLL (EPLL) employed a dc offset estimator and a Finite Impulse Response (FIR) filter to counteract dc offset was proposed in [29]. The EPLL utilized two delay operators, with a T/4 delay operator being suggested for effective dc offset rejection. Nevertheless, this PLL has some drawbacks, experiencing oscillation and exhibiting a slow transient response when dc offset was present. Furthermore, [29] lacked the presentation of a small-signal model for the FIR-PLL or a low-frequency design procedure.

To construct αβ-voltage signals in single-phase PLL, Golestan et al. generate an orthogonal signal by delaying the initial single-phase signal by 90°, and the orthogonal signal is produced (a quarter of a period). This approach is a TD based PLL method that is intended to use in single-phase SRF-PLL systems, although the delay is not precisely 90° under off-nominal frequency [10], this leads to generating an oscillation in the estimated phase angle. Smadi et al. used Variable Length TD (VLTD) to solve the oscillation problem under off-nominal frequency, and they used (DSC) operator to eliminate the DC-offset in the input of PLL [9].

Golestan et al. proposed PLLs based on adaptive and non-adoptive Cascaded DSC (CDSC). Each DSC operator is capable of rejecting disturbances in a specific way [12]. The system's lack of flexibility arises because of the utilization of a delay length equal to one-half of the fundamental grid period for reducing DC-offset.

This paper aims to propose a simple and efficient single-phase PLL method for grid synchronization that can reject DC-offset using any delay time together with its small signal model and mathematical representation. The proposed PLL was developed using TD and DSC operators with phase error compensators. Moreover, the PI controller gains were designed by creating a second-order characteristic equation. Then, the small signal model was compared to the real-time block diagram to validate the proposed PLL. Additionally, six scenarios were developed to compare the proposed PLL to other powerful PLLs to evaluate the proposed PLL. The scenarios include introducing phase jumps, DC offsets, and amplitude alterations to the grid voltage. Moreover, the variation of the grid frequency was considered.

The rest of this paper is structured as follows: Section 2 provides an overview of the methodology. Section 3 encompasses the fundamental concept, mathematical representation, small-signal model analysis, controller gain design, and a comparison of real-time and small-signal models for the proposed PLL. In Section 4, a comparison is conducted between the proposed PLL and other robust PLLs using MATLAB/Simulink. Section 5 presents the conclusions drawn from this study.

Fig. 1 Single phase SRF-PLL structure.

2 Methodology

In this work, a new method for single-phase grid synchronization with DC-offset rejection will be proposed. To achieve the objectives of this study and obtain results, the following steps will be applied:

• Present the block diagrams and conduct real-time mathematical model analysis of the proposed method.

• Mathematically derive the form of the small signal model for the proposed method.

• Development of the closed-loop transfer function for the small signal model.

• Determine the gain of the PI controller using the closed-loop transfer function.

• Verify the validity of the small signal model through analysis.

• Performing a comparative analysis between the proposed method and other robust methods to evaluate the effectiveness of the proposed PLL.

3 Development

3.1 Proposed PLL

Assume that the representation of the grid voltage with the DC offset component is:

$$v_a=V\sin \left(\theta \right)+v_a^{\mathrm{dc}},$$(1)

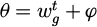where $\theta =w_g^t+\phi$ is the grid phase, V is the grid amplitude,ω_g is the grid frequency, and φ is the initial phase angle of grid voltage. 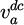$v_a^{dc}$ is the DC component in the input voltage υ_a.

According to Figure 2 the αβ reference frame voltage components (υ_a and υ_β) can be written as:

$$v_a=v_a,$$(2)

$$v_{\beta }=V\sin \left(\theta -\frac{{\omega }_g^T}{4}\right)+v_c^{dc}=-V\cos \left(\theta \right)+v_a^{dc},$$(3)

where T is a time period. The components of αβ −voltages in equations (2) and (3) that are delayed can be represented as follows:

$$\left[\begin{array}{c}\hfill v_a\left(t-\tau \right)\hfill \\ \hfill v_{\beta }\left(t-\tau \right)\hfill \end{array}\right]=V\left[\begin{array}{c}\hfill \sin \left(\theta -{\omega }_g\tau \right)\hfill \\ \hfill -\cos \left(\theta -{\omega }_g\tau \right)\hfill \end{array}\right]+\left[\begin{array}{c}\hfill v_a^{dc}\hfill \\ \hfill v_a^{dc}\hfill \end{array}\right],$$(4)

where the time delay is expressed in seconds by the symbol τ. The αβ-signals are deducted from the delayed version of the signals in the following manner to generally negate the DC-offset:

$$\left[\begin{array}{c}\hfill \mathrm{\Delta }{v}_a\hfill \\ \hfill \mathrm{\Delta }{v}_{\beta }\hfill \end{array}\right]=\left[\begin{array}{c}\hfill v_a\left(t\right)-v_a\left(t-\tau \right)\hfill \\ \hfill v_{\beta }\left(t\right)-v_{\beta }\left(t-\tau \right)\hfill \end{array}\right].$$(5)

The utilization of the delay in the PLL will cause a phase shift in the estimated phase angle, a phase error compensator has been added to the proposed PLL to solve this problem, and another phase error compensator is added to the proposed PLL to solve the oscillation problem under off-nominal frequency, Figure 1 show the proposed PLL. This approach is called Modified Transfer Delay DC-immune PLL (MTD-DCI PLL), according to Figure 1 υ_q can be written as:

$$v_q=V\left\{\begin{array}{c}\hfill -\left(\sin \left(\theta \right)-\sin \left(\theta -{\omega }_g\tau \right)\right)\sin \left(\theta -\frac{{\omega }_g\tau }{2}\right)\hfill \\ \hfill +\left(\cos \left(\theta -{\omega }_g\tau -\frac{\mathrm{\Delta }{\omega }_{g}T}{4}\right)-\cos \left(\theta -\frac{\mathrm{\Delta }{\omega }_{g}T}{4}\right)\right)\cos \left(\theta -\frac{{\omega }_g\tau }{2}+\frac{\mathrm{\Delta }{\omega }_{g}T}{4}\right)\hfill \end{array}\right\}.$$(6)

At synchronization υ_a = 0 that's means the error signal is equal to zero at synchronization and υ_a is controllable. Towered to that end, The closed-loop stability must be discussed, and the voltage controller must be designed to regulate q −axis voltage to zero. Normally, the voltage controller is a PI controller that is designed based on the PLL small signal model.

3.2 Small signal model

The estimated voltage v_a can be represented as:

$$v_q\left(t\right)=-\sin \left({\displaystyle \hat{\theta }}+{{\displaystyle \hat{\theta }}}_0\right)\mathrm{\Delta }{v}_a\left(t\right)+\cos \left({\displaystyle \hat{\theta }}+{{\displaystyle \hat{\theta }}}_0+\frac{\mathrm{\Delta }{{\displaystyle \hat{\omega }}}_{g}T}{4}\right)\mathrm{\Delta }{v}_{\beta }\left(t\right),$$(7)

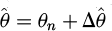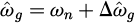where ^{^}□ is the estimated signal, ω_g = ω_n + Δω_g, ω_n is the nominal grid frequency, θ = θ_n + Δθ, ${\displaystyle \hat{\theta }}={\theta }_n+\Delta {\displaystyle \hat{\theta }}$, and ${{\displaystyle \hat{\omega }}}_g={\omega }_n+\Delta {{\displaystyle \hat{\omega }}}_g$. Equation (7) can be written as:

$$\frac{v_q\left(t\right)}{v}=\frac{1}{2}[\cos \left(\theta +\widehat{\theta }-\frac{\widehat{\omega }{g}^{\tau }}{2}\right)-\cos \left(\theta -\widehat{\theta }+\frac{\widehat{\omega }{g}^{\tau }}{2}\right)+\cos \left(\theta -\widehat{\theta }+\frac{\widehat{\omega }{g}^{\tau }}{2}-{\omega }_g\tau \right)$$

$$-\cos \left(\theta +\widehat{\theta }-\frac{{\widehat{\omega }}_g\tau }{2}-{\omega }_g\tau \right)-\cos \left(\theta -\widehat{\theta }+\frac{{\widehat{\omega }}_g\tau }{2}-\frac{\tau }{4}\left(\Delta {\omega }_g-\Delta {\widehat{\omega }}_g\right)\right)-\cos \left(\theta -\widehat{\theta }+\frac{{\widehat{\omega }}_g\tau }{2}-\frac{T}{4}\left(\Delta {\omega }_g-\Delta {\widehat{\omega }}_g\right)\right)$$

$$\cos (\theta +\widehat{\theta }-\frac{{\widehat{\omega }}_g\tau }{2}-\frac{\tau }{4}\left(\Delta {\omega }_g-\Delta {\widehat{\omega }}_g\right)-{\omega }_g\tau )+\cos \left(\theta -\widehat{\theta }+\frac{{\widehat{\omega }}_g\tau }{2}-\frac{T}{4}\left(\Delta {\omega }_g-\Delta {\widehat{\omega }}_g\right)-{\omega }_g\tau \right)]$$(8)

The double frequency terms (the highlighted terms) will cancel one another near the synchronization condition. After a few approximation operations, and by using trigonometric identities to equation (8), yields:

$$v_q\left(t\right)\approx 2V\sin \left(\frac{{\omega }_n\tau }{2}\right)\left[\frac{\mathrm{\Delta }\theta +\mathrm{\Delta }\theta -\left(\tau +\frac{T}{4}\right)\mathrm{\Delta }{\omega }_g}{2}-\mathrm{\Delta }{\displaystyle \hat{\theta }}+\left(\frac{\tau }{2}-\frac{T}{8}\right)\mathrm{\Delta }{{\displaystyle \hat{\omega }}}_g\right].$$(9)

Taking Laplace transformation to the equation (9), yields:

$$v_q\left(s\right)\approx k_l\left[\frac{1+e^{-\left(\tau +\frac{T}{4}\right)}}{2}\Delta \theta \left(s\right)-\Delta {\displaystyle \hat{\theta }}\left(s\right)-(\frac{T}{8}-\frac{\tau }{2})\Delta {{\displaystyle \hat{\omega }}}_g\left(s\right)\right]$$(10)

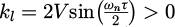where $k_l=2V\sin \left(\frac{{\omega }_n\tau }{2}\right)>0$. According to equation (10) and Figure 2, the small signal model for the MTD-DCI PLL is shown in Figure 3.

According to Figure 3, the closed-loop transfer function can be represented as:

$$G_{cl}\left(s\right)=\frac{\Delta {\displaystyle \hat{\theta }}}{\Delta \theta }=\frac{1+e^{-\left(\tau +\frac{T}{4}\right)}s}{2}\frac{k_l\left(k_p+k_i{k}_y\right)s+k_l{k}_i}{s^2+k_i\left(k_p-k_i\left(\frac{4\tau -t}{8}\right)\right)s+k_l{k}_i}$$(11)

where $k_{\gamma }=\frac{T}{4}$.

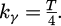3.3 PI gains design and system validation

A second-order Characteristic Equation (CE) describes the small-signal model closed-loop transfer function. Therefore, any desired output response that can be connected to a desirable natural frequency (ώ_n) and a damping factor (ζ) can be used to construct the controller gains. As a result, the desired CE can be compared to the actual CE to design the controller gains as:

$$\frac{s^2+k_i\left(k_p-k_i\left(\frac{4\tau -T}{8}\right)\right)}{2\xi {ώ}_n}s+{\displaystyle \underset{{ώ}_n^2}{{\displaystyle \underbrace{k_l{k}_i}}}}.$$

The following variables are suggested without losing generality: ξ = 0.707, ω_n = 40π rad/s, τ = 0.002 sec, and V = 1 pu, which yields k_i = 0.618. Thus, the controller gains can be calculated using equations (12) and (13).

$$k_i=\frac{{ώ}_n^2}{k_l},$$(12)

$$k_p=\frac{2\xi {ώ}_n}{k_l}+k_i\left(\frac{4\pi -T}{8}\right).$$(13)

The PI controller gains can be calculated as (k_p = 249.223) and k_i = 25551).

When a phase jump of 30° is introduced to the grid voltage at 0.02 s, the results of the small signal model and real-time simulation using Figures 2 and 3, are shown in Figure 4.

The results show that the small signal model and the real-time model responses are quite similar, demonstrating the small-signal model viability in capturing the main characteristics of the proposed PLL.

The proposed single-phase MTD DCI PLL can eliminate the effect of DC offset at any given delay time. To verify its performance, the system was evaluated through a comparison between the small signal model and the real-time model using two specific delay times, namely τ = 0.001 and τ = 0.004. At τ = 0.001, the PI controller gains were determined to be k_p = 467 and k_i = 50473, whereas, at τ = 0.004, the controller gains were found to be k_p = 144 and k_i = 13433. The results of this evaluation are presented in Figure 5 when a 30° phase jump was added to the grid voltage at 0.02 s.

The real-time model and the small signal model responses are quietly similar which validates the ability of the system for working at any delay time.

Fig. 2 Proposed MTD-DCI PLL.

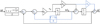Fig. 3 Small signal model for MTD-DCI PLL.

Fig. 4 Proposed MTD-DCI PLL, and its small signal model results under a phase jump of 30°.

Fig. 5 Validate the proposed method with deferent time delay.

4 Results and discussions

In this part, numerous scenarios are used to evaluate the performance of the proposed single-phase MTD-DCI PLL with the non-adaptive single-phase DSC PLL [12] shown in Figure 6, and single-phase VLTD PLL [9] shown in Figure 7. The non-adaptive single-phase DSC PLL, and the single phase VLTD PLL PI controller gains were designed in accordance with their respective small-signal models. The same (ζ) and 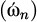$\left({ώ}_n\right)$ were used as in the proposed PLL to achieve fair comparisons. Based on its small-signal model, the single-phase non-adaptive DSC PLL PI controller gains are computed as follows: k_p = 217.193 and k_i = 15791.37, whereas the single phase VLTD-PLL gains are computed as k_p = 376.98 and k_i = 25551.

For the comparisons, the following six cases were considered:

• Adding phase jump to the grid voltage.

• Changing the grid frequency.

• Adding a DC-offset to the input voltage.

• Adding a phase jump and a DC-offset at the same time to the grid voltage.

• Changing the input voltage amplitude.

• Changing the amplitude of the grid voltage and adding a DC-offset at the same time.

MATLAB/Simulink was used to simulate the techniques. The estimated phase error and the estimated frequency for the methods were used in the comparison. The results were presented in Figures 8–19.

A. A phase jump of 30^∘ is done at 0.02 s, as indicated in Figure 8.

In this case, the results in Figure 9 show that, the proposed MTD-DCI PLL has the shortest synchronization time where when applying a phase jump of 30° the phase error becomes zero in 48.98 ms while the VLTD PLL was 49.22 ms and the non-adaptive DCS PLL was 52.91 ms. Moreover, the proposed MTD-DCI PLL shows a good estimated frequency where the peak value of the estimated frequency is 54.56 hertz (Hz) while the VLTD PLL was 54.69 Hz and the non-adaptive DSC PLL was 53.54 Hz.

B. jump in the grid frequency is done from 50 to 55 Hz at 0.02 s, as indicated in Figure 10.

In this case, the results indicate that the proposed MTD-DCI PLL outperforms the other methods in terms of synchronization time. When applying a 5 Hz jump in the grid frequency, the proposed MTD-DCI PLL achieves a zero phase error in 39.17 ms, as presented in Figure 11. In comparison, the VLTD PLL requires 41.18 ms, and the non-adaptive DCS PLL requires 58.10 ms to reach the same phase error correction. Additionally, the proposed MTD-DCI PLL demonstrates superior accuracy in estimating the frequency, with the peak value of the estimated grid frequency being 55.09 Hz. On the other hand, the VLTD PLL provides 55.18 Hz, and the DSC PLL provides 55.20 Hz as their respective peak estimated frequencies.

C. A DC-offset is added, at 0.02 s, to the grid voltage with a value of 0.2 pu, (see Fig. 12).

The proposed MTD-DCI PLL rejects the effect of the DC offset in a very short time the results in Figure 13 show that, the phase error becomes zero in 18.85 ms while the VLTD PLL was 18.85 ms and the non-adaptive DCS PLL was 52.80 ms. Moreover, the proposed MTD-DCI PLL shows a very low impact in the estimated frequency where the peak value of the estimated frequency is 50.11 Hz while the VLTD PLL was 50.11 Hz and the DSC PLL was 49.20 Hz.

D. A phase jump of 30∘ and a DC-offset of 0.15 pu are added to the grid voltage at 0.02 s, as indicated in Figure 14.

In this case, the results in Figure 15 show that the proposed MTD-DCI PLL has the shortest synchronization time where when applying a phase jump and a DC-offset to the grid voltage at the same time the phase error becomes zero in 45.49 ms while the VLTD PLL was 47.68 ms and thenon-adaptive DCS PLL was 53.03 ms. Moreover, the proposed MTD-DCI PLL shows a good estimated frequency where the peak value of the estimated frequency is 54.48 Hz while the VLTD PLL was 54.64 Hz and the DSC PLL was 53.53 Hz.

E. A jump in the amplitude of the grid voltage from 1 to 1.1 pu at 0.02 s, as indicated in Figure 16.

In this case, the results in Figure 17 show that the proposed MTD-DCI PLL has the shortest synchronization time where when a jump in the amplitude of the grid voltage was applied at 0.02 s the phase error becomes zero in 48.51 ms while the VLTD PLL was 48.51 ms and the non-adaptive DCS PLL was 56.68 ms.

F. A jump in the amplitude of the grid voltage from 1 to 1.1 pu at 0.02 s with a DC offset of 0.2 Pu added at the same time, as indicated in Figure 18.

In this particular scenario, the outcomes illustrated in Figure 19 show that the proposed MTD-DCI PLL exhibits the fastest synchronization time. When subjected to a sudden increase in grid voltage amplitude with DC-offset at 0.02 s, the phase error reaches zero in 36.62 ms. In comparison, the VLTD PLL and non-adaptive DCS PLL require 36.62 ms and 58.86 ms respectively, to achieve the same phase error correction. Moreover, the proposed MTD-DCI PLL shows the minimum estimated frequency where the peak value of the estimated frequency is 49.73 Hz while the VLTD PLL was 49.71 Hz and the DSC PLL was 49.29 Hz.

Table 1 summarizes the performance comparisons of the proposed MTD-DCI PLL with other PLLs in terms of phase settling time, and the peak of estimated frequency.

The results in Table 1 demonstrate that the proposed PLL exhibits a significantly faster response compared to the other PLLs. Particularly, in case C, when a DC-offset is added to the grid voltage, the proposed PLL quickly rejects the effect of the DC-offset without causing a significant impact on the estimated frequency. Moreover, in cases A, B, and D, the proposed PLL achieve grid voltage lock faster than the VLTD PLL and the non-adaptive DSC PLL.

Considering the comprehensive analysis of results from Figures 8–19 and Table 1, it is apparent that although the proposed MTD-DCI PLL and the VLTD PLL show fairly similar performance, the proposed MTD-DCI PLL outperforms the DSC PLL. It boasts the fastest dynamic response and achieves the shortest synchronization time over all PLLs evaluated. Another significant advantage is that the proposed PLL is not limited to any specific time delay; it effectively rejects the DC-offset at any time delays.

Overall, the study confirms that the proposed MTD-DCI PLL is a highly efficient and adaptable solution, offering quick response and accurate synchronization while different scenarios effectively.

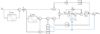Fig. 6 Non-adaptive single-phase DSC PLL.

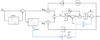Fig. 7 Single phase VLTD PLL.

Fig. 8 Grid voltage and estimated voltage under case A.

Fig. 9 Results under case A.

Fig. 10 Grid voltage and estimated voltage under case B.

Fig. 11 Results under case B.

Fig. 12 Grid voltage and estimated voltage under case C.

Fig. 13 Results under case C.

Fig. 14 Grid voltage and estimated voltage under case D.

Fig. 15 Results under case D.

Fig. 16 Grid voltage and estimated voltage under case E.

Fig. 17 Results under case E.

Fig. 18 Grid voltage and estimated voltage under case F.

Fig. 19 Results under case F.

5 Conclusions

This work suggests a way of removing the impact of the DC-offset in the grid synchronization procedure by proposing a new PLL technique based on TD and DSC operators to generate the orthogonal signal and to reject the DC-offset in the PLLs input. The proposed PLL is not constrained to a particular time delay. The proposed method incorporates a phase error compensator operator aimed at resolving phase shift problem resulting from delayed input signals. The study contains an extensive analysis of the mathematical model, small-signal model, closed-loop stability, and the process of determining the PI controller gains. To validate the small signal model, a comparison with the real-time model was performed. The PI controller gains were calculated by analyzing the real-time and small signal models, then deriving a particular second-order characteristic equation. To evaluate the efficacy of the proposed method, several scenarios were simulated using MATLAB/Simulink. The proposed method was compared with other single-phase PLLs based on performance indicators such as settling time, frequency response, and phase error. The scenarios contained the introduction of various disturbances to the input voltage, including:

• Adding Phase Jumps: Sudden shifts in phase to evaluate the PLL's ability.

• Introducing DC Offsets: Evaluating how well the PLL handles DC offset in the input voltage.

• Changing the Grid Frequency: Assessing the PLL's response to variations in grid frequency, an important factor in grid-connected systems subjected to frequency changes.

• Changing the Voltage Amplitude: Studying how the PLL responds to variations in voltage amplitude.

According to the results the proposed PLL has the fastest dynamic response and the shortest synchronization time. Due to its flexibility and benefits over other PLLs the proposed PLL is expected to be very fruitful from industrial point of view. As a direction for future research, the authors propose the development of a novel algorithm aimed at identifying optimal PI controller gains to enhance the system's speed.

Abbreviations

DG: Distributed Generators

RES: Renewable Energy Sources

PLL: Phase Locked Loop

TD: Transfer Delay

DSC: Delay Signal Cancelation

IEA: International Energy Agency

PD: Phase Detector

LF: Loop Filter

VCO: Voltage-Controlled Oscillator

IPA: Inverse Park Approach

SOGI: Second Order Generalized Integrator

KF: Kalman Filter

MAF: Moving Average Filter

A/D: Analog/Digital

SRF: Synchronous Reference Frame

APF: Active Power Filter

TD-OSG: Time Delay-based Orthogonal Signal Generator

RCE: Reference Current Extraction

DCI: DC immune

EPLL: Enhanced PLL

FIR: Finite Impulse Response

VLTD: Variable length TD

CDSC: Cascaded DSC

MTD-DCI PLL: Modified Transfer Delay DC-immune PLL

CE: Characteristic Equation

Nomenclature

υ_a: Grid voltage

θ: Grid phase

V: Grid amplitude

ω_g: Grid frequency

φ: The initial phase angle of grid voltage

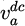$v_a^{dc}$ : DC component in the input voltage v_a

v_a, v_β: The αβ reference frame voltage components

T: Time period

τ: Delay time

v_q: The q reference frame voltage components

^{^}□: Refers to the estimated signals

ω_n: Nominal grid frequency

ώ_n: Natural frequency

ξ: Damping factor

k_p, k_i: PI controller gains

ms: Milliseconds

Hz: Hertz

pu: Per unit

Implications and influences

The aim of our research is to propose a simple and efficient single-phase phase-locked loop (PLL) method for grid synchronization that can reject DC offset. We provide a small signal model and mathematical representation of our proposed method, which was developed using transfer delay and delay signal cancelation methods with phase error compensators. Our work compares favorably with other PLLs, and we believe that our proposed PLL will have significant industrial benefits due to its flexibility and advantages.

Funding

This research received no external funding.

Conflict of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Author Contributions

Conceptualization, M.A.B.I. and P.M.B.B.; methodology, M.A.B.I. and Z.A.A.M.; software, M.A.B.I. and Z.A.A.M.; validation, P.M.B.B. and M.A.B.I.; formal analysis, M.A.B.I.; investigation, M.A.B.I. and P.M.B.B.; resources, M.A.B.I., Z.A.A.M. and P.M.B.B.; data curation, M.A.B.I. and Z.A.A.M.; writing—original draft preparation, M.A.B.I. and Z.A.A.M.; writing—review and editing, M.A.B.I. and P.M.B.B.; visualization, M.A.B.I. and P.M.B.B.; supervision, P.M.B.B.; project administration, P.M.B.B. All authors have read and agreed to the published version of the manuscript.

References

All Tables

All Figures

	Fig. 1 Single phase SRF-PLL structure.
In the text

	Fig. 2 Proposed MTD-DCI PLL.
In the text

	Fig. 3 Small signal model for MTD-DCI PLL.
In the text

	Fig. 4 Proposed MTD-DCI PLL, and its small signal model results under a phase jump of 30°.
In the text

	Fig. 5 Validate the proposed method with deferent time delay.
In the text

	Fig. 6 Non-adaptive single-phase DSC PLL.
In the text

	Fig. 7 Single phase VLTD PLL.
In the text

	Fig. 8 Grid voltage and estimated voltage under case A.
In the text

	Fig. 9 Results under case A.
In the text

	Fig. 10 Grid voltage and estimated voltage under case B.
In the text

	Fig. 11 Results under case B.
In the text

	Fig. 12 Grid voltage and estimated voltage under case C.
In the text

	Fig. 13 Results under case C.
In the text

	Fig. 14 Grid voltage and estimated voltage under case D.
In the text

	Fig. 15 Results under case D.
In the text

	Fig. 16 Grid voltage and estimated voltage under case E.
In the text

	Fig. 17 Results under case E.
In the text

	Fig. 18 Grid voltage and estimated voltage under case F.
In the text

	Fig. 19 Results under case F.
In the text